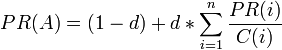31 de mayo de 2010
Puntos extra Maquina turing (Pregunta de examen de medio curso)
Lo primero que hay que hacer es convertir el 37 en numero binario.
Mi metodo es este:
37/2=18 residuo=1
18/2=9 residuo=0
9/2=4 residuo=1
4/2=2 residuo=0
2/2=1 residuo=0
Entonces tomando el divisor de la ultima division y tomando los residuos de abajo hacia arriba queda:
100101
ejecutamos la maquina turing
s
> 1 0 0 1 0 1
1- s > s, 0, -->
s
0 1 0 0 1 0 1
Cambia el inicio por un cero y avanza un espacio hacia la derecha
2- s 1 s, 1, -->
s
0 1 0 0 1 0 1
Estado "s" ,se queda el 1 y avanza a la derecha
3- s 0 s, 0,-->
s
0 1 0 0 1 0 1
Sigue estado "s", se queda el 0 y avanza un espacio a la derecha
4- s 0 s,0,-->
s
0 1 0 0 1 0 1
Sigue estado "s", se queda el cero y avanza un espacio a la derecha
5- s 1 s,1,-->
s
0 1 0 0 1 0 1
Sigue estado "s", se queda el 1 y avanza a la derecha
6- s 0 s,0,-->
s
0 1 0 0 1 0 1
Sigue estado "s", se queda el 0 y avanza hacia la derecha
7- s 1 s,1,-->
s
0 1 0 0 1 0 1
Sigue estado "s", se queda el 1 y avanza hacia la derecha y llega a un espacio vacio
8- s [_] t, 0 <--
t
0 1 0 0 1 0 1 0
Como estaba en estado "s" en una parte vacia, cambia de estado, ahora es "t", se agrega un 0 y se regresa a la izquierda un espacio.
9- t 1 t,1,<--
t
0 1 0 0 1 0 1 0
Cambia el estado "s" a "t", deja el 1 y avanza a la izquierda un espacio
10- t 0 Si, 1,--
Si
0 1 0 0 1 1 1 0
Cambia del estado "t" a "Si", cambia el 0 por el 1 y ahi se detiene
La salida de la maquina en decimal es:
1 0 0 1 1 1 0
2^6 2^5 2^4 2^3 2^2 2^1 2^0
64 0 0 8 4 2 0
64+8+4+2= 78
Que hace la maquina: pues multiplica el numero por 2 y le suma 4.
La complejidad: O(n) porque tardas segun el numero de transiciones que tienes que hacer.
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
30 de mayo de 2010
Puntos extra (Diagrama de Voronoi)
Bueno en este tema, solo les quiero compartir lo que encontre en una pagina de internet, el diagrama de voronoi es sencillo, toda la explicacion viene aqui abajo.
El diagrama de Voronoi es una de las estructuras clásicas en Geometría Computacional (disciplina encargada de resolver problemas geométricos mediante métodos algorítmicos). Es una estructura al tiempo sencilla y poderosa, que parte de una idea tan natural que ha sido descubierta varias veces a lo largo de la historia. De ahí los distintos nombres con los que ha sido conocido: diagrama de Voronoi, polígonos de Thiessen, regiones de Wigner-Seitz, etc.
Pero, ¿qué es el diagrama de Voronoi? Vamos a ilustrarlo con un ejemplo sencillo: supongamos que tenemos una empresa cuya función es ayudar a nuestros clientes a encontrar los servicios más cercanos a su situación actual. Recibimos unas coordenanas por teléfono, web, aplicación móvil... y, en el menor tiempo posible, tenemos que suministrarle la dirección del restaurante, gasolinera, parking, etc. más cercano. ¿Cómo lo hacemos?
Pensemos en el problema de manera geométrica. Partimos de un conjunto de puntos en el plano correspondientes a una categoría de servicios (por ejemplo, gasolineras). Cada consulta de nuestro cliente podemos interpretarla como un nuevo punto que tenemos que emparejar con el más cercano del conjunto inicial. ¿Cómo lo seleccionamos? Fácil, diremos: mido las distancias a cada una de las gasolineras y me quedo con la más pequeña.
Respuesta correcta, pero no del todo. Repetimos las condiciones del problema: tenemos que dar la respuesta en el menor tiempo posible. ¿Cuánto tardamos con este procedimiento? Lo que nos lleve medir la distancia a cada una de las gasolineras. No podemos hacerlo en menos tiempo porque, a priori, no podemos dejar de comprobar ninguna de ellas. ¿Significa esto que éste el mejor método entre todos los posibles?
Pues sí y no. Sí, si sólo vamos a tener unos pocos clientes; pero si esperamos que nuestra empresa sea un éxito (y con lo que nos ha constado montarla pongámonos en el mejor de los casos) y recibir miles de peticiones a cada instante, podemos hacerlo un poco mejor. Y aquí alguien ya habrá dado con la respuesta: en lugar de medir la distancia a cada una de las gasolineras hacemos una partición del plano en regiones, de tal forma que si un punto cae dentro de una determinada región entonces podemos decir cuál es su gasolinera más cercana.
Justamente eso es el diagrama de Voronoi.
O, si queremos una defición más precisa: dado un conjunto S de generadores en el plano, el diagrama de Voronoi de S es la partición del plano tal que a cada punto de S le asigna la región formada por los puntos del plano que están más cerca suya que de cualquier otro elemento de S.
Construir el diagrama no es más rápido que medir la distancia a cada gasolinera. Nada (que funcione) es más rápido que eso. Pero si bien construir el diagrama es más lento, sólo tenemos que hacerlo una vez, y a partir de ahí determinar en qué región está un punto sí puede hacerse antes. Y ahí está el quid de la cuestión. Gastamos un poco más de tiempo al inicio, pero luego nuestras búsquedas serán mucho más rápidas (que es lo que nos exigen nuestros clientes).
Bibliografia:
http://lacanciondemalapata.blogspot.com/2010/02/el-diagrama-de-voronoi-i.html
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
El diagrama de Voronoi es una de las estructuras clásicas en Geometría Computacional (disciplina encargada de resolver problemas geométricos mediante métodos algorítmicos). Es una estructura al tiempo sencilla y poderosa, que parte de una idea tan natural que ha sido descubierta varias veces a lo largo de la historia. De ahí los distintos nombres con los que ha sido conocido: diagrama de Voronoi, polígonos de Thiessen, regiones de Wigner-Seitz, etc.
Pero, ¿qué es el diagrama de Voronoi? Vamos a ilustrarlo con un ejemplo sencillo: supongamos que tenemos una empresa cuya función es ayudar a nuestros clientes a encontrar los servicios más cercanos a su situación actual. Recibimos unas coordenanas por teléfono, web, aplicación móvil... y, en el menor tiempo posible, tenemos que suministrarle la dirección del restaurante, gasolinera, parking, etc. más cercano. ¿Cómo lo hacemos?
Pensemos en el problema de manera geométrica. Partimos de un conjunto de puntos en el plano correspondientes a una categoría de servicios (por ejemplo, gasolineras). Cada consulta de nuestro cliente podemos interpretarla como un nuevo punto que tenemos que emparejar con el más cercano del conjunto inicial. ¿Cómo lo seleccionamos? Fácil, diremos: mido las distancias a cada una de las gasolineras y me quedo con la más pequeña.
Respuesta correcta, pero no del todo. Repetimos las condiciones del problema: tenemos que dar la respuesta en el menor tiempo posible. ¿Cuánto tardamos con este procedimiento? Lo que nos lleve medir la distancia a cada una de las gasolineras. No podemos hacerlo en menos tiempo porque, a priori, no podemos dejar de comprobar ninguna de ellas. ¿Significa esto que éste el mejor método entre todos los posibles?
Pues sí y no. Sí, si sólo vamos a tener unos pocos clientes; pero si esperamos que nuestra empresa sea un éxito (y con lo que nos ha constado montarla pongámonos en el mejor de los casos) y recibir miles de peticiones a cada instante, podemos hacerlo un poco mejor. Y aquí alguien ya habrá dado con la respuesta: en lugar de medir la distancia a cada una de las gasolineras hacemos una partición del plano en regiones, de tal forma que si un punto cae dentro de una determinada región entonces podemos decir cuál es su gasolinera más cercana.
Justamente eso es el diagrama de Voronoi.
O, si queremos una defición más precisa: dado un conjunto S de generadores en el plano, el diagrama de Voronoi de S es la partición del plano tal que a cada punto de S le asigna la región formada por los puntos del plano que están más cerca suya que de cualquier otro elemento de S.
Construir el diagrama no es más rápido que medir la distancia a cada gasolinera. Nada (que funcione) es más rápido que eso. Pero si bien construir el diagrama es más lento, sólo tenemos que hacerlo una vez, y a partir de ahí determinar en qué región está un punto sí puede hacerse antes. Y ahí está el quid de la cuestión. Gastamos un poco más de tiempo al inicio, pero luego nuestras búsquedas serán mucho más rápidas (que es lo que nos exigen nuestros clientes).
Bibliografia:
http://lacanciondemalapata.blogspot.com/2010/02/el-diagrama-de-voronoi-i.html
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
Puntos extra (Algoritmo de Euclides)
El algoritmo de Euclides es un método antiguo y eficaz para calcular el máximo común divisor (MCD). Fue originalmente descrito por Euclides en su obra Elementos. El algoritmo de Euclides extendido es una ligera modificación que permite además expresar al máximo común divisor como una combinación lineal. Este algoritmo tiene aplicaciones en diversas áreas como álgebra, teoría de números y ciencias de la computación entre otras. Con unas ligeras modificaciones suele ser utilizado en computadoras electrónicas debido a su gran eficiencia.
Al dividir a entre b (números enteros), se obtiene un cociente q y un residuo r. Es posible demostrar que el máximo común divisor de a y b es el mismo que el de b y r. Éste es el fundamento principal del algoritmo. También es importante tener en cuenta que el máximo común divisor de cualquier número a y 0 es precisamente a. Para fines prácticos, la notación mcd(a,b) significa máximo común divisor de a y b.
Según lo antes mencionado, para calcular el máximo común divisor de 2366 y 273 se puede proseguir de la siguiente manera:
Paso Operación Significado
1 2366 dividido entre 273 es 8 y sobran 182 mcd(2366,273) = mcd(273,182)
2 273 dividido entre 182 es 1 y sobran 91 mcd(273,182) = mcd(182,91)
3 182 dividido entre 91 es 2 y sobra 0 mcd(182,91) = mcd(91,0)
La secuencia de igualdades mcd(2366,273) = mcd(273,182) = mcd(182,91) = mcd(91,0) implican que mcd(2366,273) = mcd(91,0). Dado que mcd(91,0) = 91, entonces se concluye que mcd(2366,273) = 91. Este mismo procedimiento se puede aplicar a cualesquiera dos números naturales. En general, si se desea encontrar el máximo común divisor de dos números naturales a y b, se siguen las siguientes reglas:
1.Si b = 0 entonces mcd(a,b) = a y el algoritmo termina
2.En otro caso, mcd(a,b) = mcd(b,r) donde r es el resto de dividir a entre b. Para calcular mcd(b,r) se utilizan estas mismas reglas.
Aqui tenemos el pseudocodigo:
Función mcd(a,b):
Mientras
haga lo siguiente:
El resultado es a
Otro ejemplo sencillo:
MCD 12345 y 6789
12345mod789= 510
789mod510=279
510mod279=231
279mod231=48
231mod48=39
48mod39=9
39mod9=3
9mod3=0
MCD (3,0) entonces como tenemos b=0, el MCD es a=3.
Como vemos este es un algoritmo sencillo para obtener el MCD de dos numeros.
Complejidad: El teorema de Lamé afirma que el caso peor para este algoritmo es cuando se le pide calcular el máximo común divisor de dos números consecutivos de la sucesión de Fibonacci. En general, el número de divisiones efectuadas por el algoritmo nunca supera 5 veces el número de dígitos que tienen estos números. En términos de complejidad computacional, esto significa que se requieren
divisiones para calcular el máximo común divisor de n y m donde n> m.
El número promedio de divisiones efectuadas por el algoritmo se estuvo investigando desde 1968, pero sólo hasta apenas el año 2002, Brigitte Vallée demostró que si los dos números se pueden representar con n bits, entonces el número promedio de divisiones necesarias es:
Sin embargo, no basta con saber el número de divisiones. Hay que recordar que el algoritmo de Euclides funciona tanto para polinomios como para números enteros, y en general, cualquier dominio Euclídeo. En cada caso, la complejidad del algoritmo depende del número de divisiones efectuadas y del costo de cada división. En el caso de los polinomios, el número de divisiones es 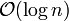 donde n es el grado de los polinomios.
donde n es el grado de los polinomios.
Bibliografia:
http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
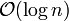 donde n es el grado de los polinomios.
donde n es el grado de los polinomios.Bibliografia:
http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
Puntos extra (Distancia de edicion)
En Teoría de la información y Ciencias de la Computación se llama Distancia de Levenshtein, distancia de edición, o distancia entre palabras, al número mínimo de operaciones requeridas para transformar una cadena de caracteres en otra. Se entiende por operación, bien una inserción, eliminación o la sustitución de un carácter. Esta distancia recibe ese nombre en honor al científico ruso Vladimir Levenshtein, quien se ocupara de esta distancia en 1965. Es útil en programas que determinan cuán similares son dos cadenas de caracteres, como es el caso de los correctores de ortografía.
Es usual hablar de distancia o diferencias entre objetos, es por ello que no resulta extraño el término distancia o medida de similitud entre dos cadenas.
Al hablar de distancia entre cadenas se estaría hablando de medir las diferencias que hay entre estas. Algunas de las diferencias interesantes podrían ser encontradas en las longitudes de las cadenas que se están comparando, o, en palabras de una misma longitud los cambios de unas letras por otras.
Esta métrica ha sido utilizada en la solución de diversos problemas, sobre todo en los de procesamiento de textos o del lenguaje natural.
Los procesadores de textos de última generación son capaces de sugerir posibles palabras que pueden servir de reemplazo para una palabra encontrada en un textocon errores ortográficos. Estos procesadores saben cómo evaluar la distancia entre una palabra mal escrita y palabras que ya se encuentran almacenadas en sus ficheros o diccionarios; aquellas palabras cuyas distancias evaluadas son la más pequeñas, son ofrecidas como candidatas para el reemplazo.
La "Distancia Levenshtein" o "Distancia de Edición", como también se le conoce a esta métrica, es el número de eliminaciones, inserciones o sustituciones requeridas para transformar una cadena fuente "x" en una cadena objetivo "z".
Por ejemplo:
•Si x = "mesa" y z = "mesa", entonces DL (x,z) = 0, porque no es necesario hacer ninguna transformación. Las cadenas fuente y objetivo son idénticas.
•Si x = "enojo" y z = "enajo", entonces DL (x,z) = 1, porque es necesaria una transformación para que la cadena fuente y objetivo sean iguales (cambiar la "o" por la "a").
•Si x = "enojo" y z = "enojar", entonces DL (x,z) = 2, porque son necesarias dos transformaciones para que la cadena fuente y objetivo sean iguales (insertar la "r" al final de la palabra fuente y cambiar la "o" por la "a").
Algunas aplicaciones en la que se puede usar la distancia de edicion son:
1.Sistemas para la revisión de faltas ortográficas automatizada en textos.
2.Sistemas de reconocimiento de voz.
3.Sistemas para el análisis de ADN.
4.Sistemas para la detección de plagios.
Aqui esta un pequeño ejemplo: Convertir la palabra gato a perro
Al sustituir, insertar o eliminar vas a agregar un uno a la suma y si es la misma letra en fila y columna no se suma, se queda igual.
Tu al principio en la segunda columna despues de la palabra "gato" donde esta el unico 0 vas a poner hacia abajo la serie del 0 a "n "de uno en uno, n es la cantidad de letras que tiene la palabra, como en la imagen de arriba "gato" tiene 4 letras, se pone en la segunda columna: 0,1,2,3,4.
Despues en la segunda fila abajo de "perro", despues del 0 vas poner otra ves la misma serie empezando de ese cero hasta "n", como "perro" tiene 5 letras se pone 0,1,2,3,4,5.
A continuacion en la columna de la letra "G" y fila "P" como vemos que son letras distintas vamos a tomar el 0 que esta en la celda donde no hay letra en columna y fila y le vamos a sumar un 1, y ponemos en la celda ese 1.
Despues bajamos a la fila "A" pero seguimos en la columna "G", son letras distintas entonces se le va sumar 1 al numero que esta abajo del cero y al lado de la letra "G" que viene siendo 1, entonces lo sumamos y queda 2 que es lo que se pone en la celda.
Despues bajamos a la fila "T" en la misma columna "G", son letras distintas entonces se le va a sumar 1 al numero que esta debajo del 1 que usamos en el paso anterior, es el 2, entonces 2 + 1= 3, el 3 se pone en la interseccion de "T" y "G". Asi sucesivamente sigues estos pasos, hasta que acabes la columna con todas las letras, despues sigue la siguiente columna con todas las letras, pero ahora sumandole los elementos de la columna que acabas de terminar. Por ejemplo estas en la columna "E" y fila "G", son letras distintas entonces le suma 1, tomas el elemento a la derecha del 0 del principio de la tabla, es el 1, entonces 1 + 1= 2, el 2 se pone en la celda "EyG". Asi sigues hasta completar la tabla, pero cuidado cuando tienes la misma letra en fila y columna no se suma nada, se pasa el elemento que esta en la parte superior izquierda de esa intersecion de fila y columna y se pone en esa celda. Por ejemplo en la tabla de arriba tenemos la columna "O" y fila "O", son iguales y por lo tanto no sumas nada, entonces agarras el numero en la parte superior izquierda de esa celda, viene siendo el 4, entonces se pasa ese mismo 4 a la celda que en esta tabla es la celda final. Tomas el valor de esa celda final de la tabla como el numero de la distancia de edicion que hay entre estas cadenas de caracteres, esta marcado en verde.
Necesitas 4 transformaciones para convertir de gato a perro. Entiendase por transformaciones las sustituciones, inserciones y eliminaciones de caracteres.
Bibliografia:
http://es.wikipedia.org/wiki/Distancia_de_Levenshtein
http://www.monografias.com/trabajos34/similitud/similitud.shtml
Es usual hablar de distancia o diferencias entre objetos, es por ello que no resulta extraño el término distancia o medida de similitud entre dos cadenas.
Al hablar de distancia entre cadenas se estaría hablando de medir las diferencias que hay entre estas. Algunas de las diferencias interesantes podrían ser encontradas en las longitudes de las cadenas que se están comparando, o, en palabras de una misma longitud los cambios de unas letras por otras.
Esta métrica ha sido utilizada en la solución de diversos problemas, sobre todo en los de procesamiento de textos o del lenguaje natural.
Los procesadores de textos de última generación son capaces de sugerir posibles palabras que pueden servir de reemplazo para una palabra encontrada en un textocon errores ortográficos. Estos procesadores saben cómo evaluar la distancia entre una palabra mal escrita y palabras que ya se encuentran almacenadas en sus ficheros o diccionarios; aquellas palabras cuyas distancias evaluadas son la más pequeñas, son ofrecidas como candidatas para el reemplazo.
La "Distancia Levenshtein" o "Distancia de Edición", como también se le conoce a esta métrica, es el número de eliminaciones, inserciones o sustituciones requeridas para transformar una cadena fuente "x" en una cadena objetivo "z".
Por ejemplo:
•Si x = "mesa" y z = "mesa", entonces DL (x,z) = 0, porque no es necesario hacer ninguna transformación. Las cadenas fuente y objetivo son idénticas.
•Si x = "enojo" y z = "enajo", entonces DL (x,z) = 1, porque es necesaria una transformación para que la cadena fuente y objetivo sean iguales (cambiar la "o" por la "a").
•Si x = "enojo" y z = "enojar", entonces DL (x,z) = 2, porque son necesarias dos transformaciones para que la cadena fuente y objetivo sean iguales (insertar la "r" al final de la palabra fuente y cambiar la "o" por la "a").
Algunas aplicaciones en la que se puede usar la distancia de edicion son:
1.Sistemas para la revisión de faltas ortográficas automatizada en textos.
2.Sistemas de reconocimiento de voz.
3.Sistemas para el análisis de ADN.
4.Sistemas para la detección de plagios.
Aqui esta un pequeño ejemplo: Convertir la palabra gato a perro
Al sustituir, insertar o eliminar vas a agregar un uno a la suma y si es la misma letra en fila y columna no se suma, se queda igual.
Tu al principio en la segunda columna despues de la palabra "gato" donde esta el unico 0 vas a poner hacia abajo la serie del 0 a "n "de uno en uno, n es la cantidad de letras que tiene la palabra, como en la imagen de arriba "gato" tiene 4 letras, se pone en la segunda columna: 0,1,2,3,4.
Despues en la segunda fila abajo de "perro", despues del 0 vas poner otra ves la misma serie empezando de ese cero hasta "n", como "perro" tiene 5 letras se pone 0,1,2,3,4,5.
A continuacion en la columna de la letra "G" y fila "P" como vemos que son letras distintas vamos a tomar el 0 que esta en la celda donde no hay letra en columna y fila y le vamos a sumar un 1, y ponemos en la celda ese 1.
Despues bajamos a la fila "A" pero seguimos en la columna "G", son letras distintas entonces se le va sumar 1 al numero que esta abajo del cero y al lado de la letra "G" que viene siendo 1, entonces lo sumamos y queda 2 que es lo que se pone en la celda.
Despues bajamos a la fila "T" en la misma columna "G", son letras distintas entonces se le va a sumar 1 al numero que esta debajo del 1 que usamos en el paso anterior, es el 2, entonces 2 + 1= 3, el 3 se pone en la interseccion de "T" y "G". Asi sucesivamente sigues estos pasos, hasta que acabes la columna con todas las letras, despues sigue la siguiente columna con todas las letras, pero ahora sumandole los elementos de la columna que acabas de terminar. Por ejemplo estas en la columna "E" y fila "G", son letras distintas entonces le suma 1, tomas el elemento a la derecha del 0 del principio de la tabla, es el 1, entonces 1 + 1= 2, el 2 se pone en la celda "EyG". Asi sigues hasta completar la tabla, pero cuidado cuando tienes la misma letra en fila y columna no se suma nada, se pasa el elemento que esta en la parte superior izquierda de esa intersecion de fila y columna y se pone en esa celda. Por ejemplo en la tabla de arriba tenemos la columna "O" y fila "O", son iguales y por lo tanto no sumas nada, entonces agarras el numero en la parte superior izquierda de esa celda, viene siendo el 4, entonces se pasa ese mismo 4 a la celda que en esta tabla es la celda final. Tomas el valor de esa celda final de la tabla como el numero de la distancia de edicion que hay entre estas cadenas de caracteres, esta marcado en verde.
Necesitas 4 transformaciones para convertir de gato a perro. Entiendase por transformaciones las sustituciones, inserciones y eliminaciones de caracteres.
Bibliografia:
http://es.wikipedia.org/wiki/Distancia_de_Levenshtein
http://www.monografias.com/trabajos34/similitud/similitud.shtml
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
16 de mayo de 2010
Proyecto V
Bueno el tema que escogi para este proyecto V fue "Arboles de expansion: algoritmo de Kruskal.
Bueno para entender mejor sobre los arboles de expansion y algoritmo de kruskal tenemos estas definiciones:
¿Que es un arbol de expansion? Un árbol de expansión T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas) de las aristas de G. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que cubre todos los vértices. Esto es, cada vértice está en el árbol, pero no hay ciclos.
¿Que es el algoritmo de Kruskal? Esta es la definicion: El algoritmo de Kruskal es un algoritmo de la teoría de grafos para encontrar un árbol de expansión mínimo en un grafo conexo y ponderado. Es decir, busca un subconjunto de aristas que, formando un árbol, incluyen todos los vértices y no hay ciclos y donde el valor total de todas las aristas del árbol es el mínimo, a esto se le llama arbol de expansion minimo. El algoritmo de Kruskal es un ejemplo de algoritmo voraz. Esta definicion en términos simples es como encontrar el arbol de expansion pero que el peso total de las aristas sea el menor posible.
Bueno ahora ¿que es un algoritmo voraz? Un algoritmo voraz es un algoritmo que trabaja por etapas, en cada una de estas etapas toma la decisión que le parece mejor para encontrar una solución optima en cada etapa sin pensar en las consecuencias futuras, esto hace que si en cada etapa hay una solución optima, supone que habrá una solución optima global del problema.
Pero no siempre es así, no todos los problemas pueden ser resueltos por este tipo de algoritmos. La estrategia de este tipo de algoritmos consiste en tratar de ganar todas las batallas sin pensar que para ganar la guerra muchas veces es necesario perder alguna batalla. Pero para este tipo de problemas siempre hay una solución optima.
Ya vimos todas las definiciones pero para que nos sirve el algoritmo de kruskal, sabemos que con el podemos encontrar el arbol de expansion minimo pero para que nos sirve esto en la vida cotidiana. La aplicación típica de este problema es el diseño de redes telefónicas. Un ejemplo seria: Una empresa con diferentes oficinas, trata de trazar líneas de teléfono para conectarlas unas con otras.La compañía telefónica le ofrece esta interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La formulación del árbol de expansion minimo también ha sido aplicada para hallar soluciones en diversas áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones - TV por cable, sistemas distribuidos, interpretación de datos climatológicos, visión artificial - análisis de imágenes - extracción de rasgos de parentesco, análisis de clusters y búsqueda de superestructuras de quasar, plegamiento de proteínas, reconocimiento de células cancerosas, y otros).
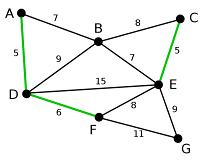
A continuacion tenemos el ejemplo a paso a paso de como funciona este algoritmo:
La siguiente arista, DF con peso 6, ha sido resaltada utilizando el mismo método.
La siguientes aristas más pequeñas son AB y BE, ambas con peso 7. AB se elige arbitrariamente, y se resalta. La arista BD se resalta en rojo, porque formaría un ciclo ABD si se hubiera elegido.
El proceso continúa marcando las aristas, BE con peso 7. Muchas otras aristas se marcan en rojo en este paso: BC (formaría el ciclo BCE), DE (formaría el ciclo DEBA), y FE (formaría el ciclo FEBAD).
Finalmente, el proceso termina con la arista EG de peso 9, y se ha encontrado el árbol de expansion mínimo.
Aqui tenemos un video de youtube que nos pueden ayudar a comprender mejor el tema
Ignorando los vértices aislados, los cuales forman su propia componente del árbol de expansión mínimo, n ≤ 2m, así que log n es O(log m).Se puede conseguir esta complejidad de la siguiente manera: primero se ordenan las aristas por su peso usando una ordenación por comparación (comparison sort) con una complejidad del orden de O(m log m); esto permite que el paso "eliminar una arista de peso mínimo de C" se ejecute en tiempo constante. Lo siguiente es usar una estructura de datos sobre conjuntos disjuntos para controlar qué vértices están en qué componentes. Es necesario hacer orden de O(m) operaciones ya que por cada arista hay dos operaciones de búsqueda y posiblemente una unión de conjuntos. Incluso una estructura de datos sobre conjuntos disjuntos simple con uniones por rangos puede ejecutar las operaciones mencionadas en O(m log n). Por tanto, la complejidad total es del orden de O(m log m) = O(m log n).
---Ahora tenemos el pseudocodigo:
Se crea un bosque B (un conjunto de árboles), donde cada vértice del grafo es un árbol separado.
Se crea un conjunto C que contenga a todas las aristas del grafo.
Mientras C es no vacío .
Eliminar una arista de peso mínimo de C.
Si esa arista conecta dos árboles diferentes se añade al bosque, combinando los dos árboles en un solo árbol.
En caso contrario, se desecha la arista.
Al acabar el algoritmo, el bosque tiene un solo componente, el cual forma un árbol de expansión mínimo del grafo.
---Estructuras que utiliza
Pues este algoritmo usa arreglos, árboles por supuesto
Bibliografia:
Bueno para entender mejor sobre los arboles de expansion y algoritmo de kruskal tenemos estas definiciones:
¿Que es un arbol de expansion? Un árbol de expansión T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas) de las aristas de G. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que cubre todos los vértices. Esto es, cada vértice está en el árbol, pero no hay ciclos.
Aqui hay una imagen de un arbol de expansion
Bueno ahora ¿que es un algoritmo voraz? Un algoritmo voraz es un algoritmo que trabaja por etapas, en cada una de estas etapas toma la decisión que le parece mejor para encontrar una solución optima en cada etapa sin pensar en las consecuencias futuras, esto hace que si en cada etapa hay una solución optima, supone que habrá una solución optima global del problema.
Pero no siempre es así, no todos los problemas pueden ser resueltos por este tipo de algoritmos. La estrategia de este tipo de algoritmos consiste en tratar de ganar todas las batallas sin pensar que para ganar la guerra muchas veces es necesario perder alguna batalla. Pero para este tipo de problemas siempre hay una solución optima.
Ya vimos todas las definiciones pero para que nos sirve el algoritmo de kruskal, sabemos que con el podemos encontrar el arbol de expansion minimo pero para que nos sirve esto en la vida cotidiana. La aplicación típica de este problema es el diseño de redes telefónicas. Un ejemplo seria: Una empresa con diferentes oficinas, trata de trazar líneas de teléfono para conectarlas unas con otras.La compañía telefónica le ofrece esta interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La formulación del árbol de expansion minimo también ha sido aplicada para hallar soluciones en diversas áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones - TV por cable, sistemas distribuidos, interpretación de datos climatológicos, visión artificial - análisis de imágenes - extracción de rasgos de parentesco, análisis de clusters y búsqueda de superestructuras de quasar, plegamiento de proteínas, reconocimiento de células cancerosas, y otros).
A continuacion tenemos el ejemplo a paso a paso de como funciona este algoritmo:
Este es el grafo original. Los números de las aristas indican su peso. Ninguna de las aristas está resaltada.
AD y CE son las aristas más cortas, con peso 5, y AD se ha elegido arbitrariamente, por tanto se resalta.
Sin embargo, ahora es CE la arista más pequeña que no forma ciclos, con peso 5, por lo que se resalta como segunda arista.
La siguiente arista, DF con peso 6, ha sido resaltada utilizando el mismo método.
La siguientes aristas más pequeñas son AB y BE, ambas con peso 7. AB se elige arbitrariamente, y se resalta. La arista BD se resalta en rojo, porque formaría un ciclo ABD si se hubiera elegido.
El proceso continúa marcando las aristas, BE con peso 7. Muchas otras aristas se marcan en rojo en este paso: BC (formaría el ciclo BCE), DE (formaría el ciclo DEBA), y FE (formaría el ciclo FEBAD).
Finalmente, el proceso termina con la arista EG de peso 9, y se ha encontrado el árbol de expansion mínimo.
Aqui tenemos un video de youtube que nos pueden ayudar a comprender mejor el tema
---Ahora sigue su definicion formal en problema de decision:
¿Puede el algoritmo de Kruskal encontrar siempre el arbol de expansion minima? R= si
Segun lo que definimos anteriormente el algoritmo de Kruskal siempre tiene una solucion optima a este tipo de problemas donde se busca el arbol de expansion minimo eso quiere decir que este algoritmo pertenece a P porque se puede resolver de forma eficiente por una maquina determinista en tiempo polinomial.
---Analisis asintotico:
m el número de aristas del grafo y n el número de vértices, el algoritmo de Kruskal muestra una complejidad O(m log m) o, equivalentemente, O(m log n), cuando se ejecuta sobre estructuras de datos simples. Los tiempos de ejecución son equivalentes porque:
m es a lo sumo n2 y log n2 = 2logn es O(log n).Ignorando los vértices aislados, los cuales forman su propia componente del árbol de expansión mínimo, n ≤ 2m, así que log n es O(log m).Se puede conseguir esta complejidad de la siguiente manera: primero se ordenan las aristas por su peso usando una ordenación por comparación (comparison sort) con una complejidad del orden de O(m log m); esto permite que el paso "eliminar una arista de peso mínimo de C" se ejecute en tiempo constante. Lo siguiente es usar una estructura de datos sobre conjuntos disjuntos para controlar qué vértices están en qué componentes. Es necesario hacer orden de O(m) operaciones ya que por cada arista hay dos operaciones de búsqueda y posiblemente una unión de conjuntos. Incluso una estructura de datos sobre conjuntos disjuntos simple con uniones por rangos puede ejecutar las operaciones mencionadas en O(m log n). Por tanto, la complejidad total es del orden de O(m log m) = O(m log n).
---Ahora tenemos el pseudocodigo:
Se crea un bosque B (un conjunto de árboles), donde cada vértice del grafo es un árbol separado.
Se crea un conjunto C que contenga a todas las aristas del grafo.
Mientras C es no vacío .
Eliminar una arista de peso mínimo de C.
Si esa arista conecta dos árboles diferentes se añade al bosque, combinando los dos árboles en un solo árbol.
En caso contrario, se desecha la arista.
Al acabar el algoritmo, el bosque tiene un solo componente, el cual forma un árbol de expansión mínimo del grafo.
---Estructuras que utiliza
Pues este algoritmo usa arreglos, árboles por supuesto
Bibliografia:
Enlace a la presentacion interactiva:
http://rapidshare.com/files/387870056/arboles_de_expansi__n--_algoritmo_de_Kruskal.ppt.html
Juan Manuel Casanova Villarreal
Matricula: 1453829
Juan Manuel Casanova Villarreal
Matricula: 1453829
25 de abril de 2010
Proyecto IV
Bueno en este proyecto IV nos toco el tema de ordenamiento por mezcla (mergesort) para arreglos.
Definire lo que es mergesort: La ordenacion por mezcla (MergeSort) utiliza la técnica de Divide y Vencerás para el ordenamiento de sus datos. La técnica de Divide y Vencerás utiliza basicamente tres pasos:
1. Divide: Dividir el problema en un cierto número de subproblemas.
2. Vence: Soluciona los problemas de manera recursiva. Si el tamaño de los subproblemas es suficientemente pequeño, simplemente resuelvelos de la manera mas obvia.
3. Combina: Combina el resultado de los subproblemas para obtener la solución al problema original.
La ordenación por mezcla se apega estrictamente a la técnica. La idea del algoritmo es la siguiente:
1. Divide: Divide la secuencia de n elementos en dos subsecuencias de n/2 elementos.
2. Vence: Ordena ambas subsecuencias de manera recursiva.
3. Combina: Mezcla las dos subsecuencias ordenadas para obtener la solución del problema.
Para la solución recursiva cada subsecuencia a su vez se divide en dos sub-subsecuencias, y así hasta obtener una subsecuencia de tamaño 1, en este momento se detienen la recursión, ya que una subsecuencia de tamaño uno, siempre está ordenada. Su complejidad es O(n log n).
*Que hice yo: bueno lo que yo hice fue ayudar en la busqueda de informacion en la introduccion de la clase y las aplicaciones reales.
*Como me salio: pues bien, la informacion fue encontrada rapidamente.
*En que aspectos estoy bien y en que me hace falta mejorar: pues en lo que creo que estoy bien es en ser responsable y hacer lo que me toco de investigacion, en lo que me hace falta mejorar es en dedicar un poco mas de tiempo para comprender el problema.
*Ayudo en los demas o me apoyo en ellos: pues son las dos cosas a la ves, ayudo a los demas a resolver ciertas dudas y ellos me apoyan a mi para resolver mis dudas, todo es trabajo en equipo.
*Quien se encarga de coordinar el trabajo: pues mi compañero Elias fue el que coordino el trabajo, nos dijo que nos juntaramos un cierto dia en el que todos pudieramos estar presentes para realizar el proyecto y el nos asignó lo que nos tocaba investigar.
*Que papel tomo yo: pues de alguien que ayuda a sus compañeros de equipo y que es ayudado por ellos en la realizacion de este proyecto, y de alguien que cumple con la parte del trabajo que le tocó.
Bueno, estos son los enlaces a los blogs de mis compañeros de equipo:
http://dariomtz.blogspot.com/ Dario Martinez
http://www.elias1218.mibitacora.com/ Elias Ganem
http://www.gonzalomarroquinrdz.blogspot.com/ Jesus Gonzalo
Este es el enlace a la diapositivas:
http://rapidshare.com/files/380200196/Ordenamiento_por_mezcla__mergesort__para_arreglos.pptx.html
Definire lo que es mergesort: La ordenacion por mezcla (MergeSort) utiliza la técnica de Divide y Vencerás para el ordenamiento de sus datos. La técnica de Divide y Vencerás utiliza basicamente tres pasos:
1. Divide: Dividir el problema en un cierto número de subproblemas.
2. Vence: Soluciona los problemas de manera recursiva. Si el tamaño de los subproblemas es suficientemente pequeño, simplemente resuelvelos de la manera mas obvia.
3. Combina: Combina el resultado de los subproblemas para obtener la solución al problema original.
La ordenación por mezcla se apega estrictamente a la técnica. La idea del algoritmo es la siguiente:
1. Divide: Divide la secuencia de n elementos en dos subsecuencias de n/2 elementos.
2. Vence: Ordena ambas subsecuencias de manera recursiva.
3. Combina: Mezcla las dos subsecuencias ordenadas para obtener la solución del problema.
Para la solución recursiva cada subsecuencia a su vez se divide en dos sub-subsecuencias, y así hasta obtener una subsecuencia de tamaño 1, en este momento se detienen la recursión, ya que una subsecuencia de tamaño uno, siempre está ordenada. Su complejidad es O(n log n).
*Que hice yo: bueno lo que yo hice fue ayudar en la busqueda de informacion en la introduccion de la clase y las aplicaciones reales.
*Como me salio: pues bien, la informacion fue encontrada rapidamente.
*En que aspectos estoy bien y en que me hace falta mejorar: pues en lo que creo que estoy bien es en ser responsable y hacer lo que me toco de investigacion, en lo que me hace falta mejorar es en dedicar un poco mas de tiempo para comprender el problema.
*Ayudo en los demas o me apoyo en ellos: pues son las dos cosas a la ves, ayudo a los demas a resolver ciertas dudas y ellos me apoyan a mi para resolver mis dudas, todo es trabajo en equipo.
*Quien se encarga de coordinar el trabajo: pues mi compañero Elias fue el que coordino el trabajo, nos dijo que nos juntaramos un cierto dia en el que todos pudieramos estar presentes para realizar el proyecto y el nos asignó lo que nos tocaba investigar.
*Que papel tomo yo: pues de alguien que ayuda a sus compañeros de equipo y que es ayudado por ellos en la realizacion de este proyecto, y de alguien que cumple con la parte del trabajo que le tocó.
Bueno, estos son los enlaces a los blogs de mis compañeros de equipo:
http://dariomtz.blogspot.com/ Dario Martinez
http://www.elias1218.mibitacora.com/ Elias Ganem
http://www.gonzalomarroquinrdz.blogspot.com/ Jesus Gonzalo
Este es el enlace a la diapositivas:
http://rapidshare.com/files/380200196/Ordenamiento_por_mezcla__mergesort__para_arreglos.pptx.html
21 de marzo de 2010
Proyecto III
Este es el proyecto III que habla del tema de recursion.
Definiré con mis propias palabras el termino recursion: bueno yo entendi que recursion es cuando un algoritmo se llama a si mismo dentro de ese algoritmo para completar un proceso, es decir, el algoritmo se divide en partes y se llama a la operacion para que haga los problemas de cada parte hasta que ya no queda nada que resolver y termina el algoritmo y sirve para resolver ciertos problemas como el maximo comun divisor (mcd) que es el tema que nos toco de este proyecto. La recursion segun lo que investigue en algoritmos que ocupan mucha memoria no es muy bueno porque como se divide el algoritmo en partes, el programa utiliza memoria para cada parte entonces el algoritmo ocuparia demasiada memoria.
Bueno como les dije anteriormente nos toco el proyecto del "Maximo Comun Divisor" (mcd).
Como trabajamos en grupo:
Bueno todos nos dividimos el trabajo en partes y cada quien hizo su trabajo, despues mis compañeros me enviaron lo que hicieron y yo lo puse en una presentación. Fue un proyecto facil porque todos trabajos en equipo y nos ayudabamos a resolver nuestras dudas.
Que fue mi contribucion al trabajo:
Mi contribucion fue hacer la presentacion en Powerpoint con todos los temas, ademas de hacer lo de los algoritmos iterativos y recursivos y hacer los ejemplos de ejecucion paso a paso y ayudar a mis compañeros en lo del analisis asintotico y algunas dudas mas.
Como compara lo que hice con lo que hicieron mis compañeros:
Bueno como dije anteriormente, todos nos dividimos el trabajo pero por falta de tiempo y planificacion a algunos les toco menos trabajo que hacer o mas trabajo.
Que podria mejorar en el futuro:
Como equipo podriamos mejor la planificacion del tiempo, empezar antes, para que no se nos juntara todo el trabajo en un solo dia.
Ligas a los blogs de mis compañeros:
Ernesto Mendez Govea
Alberto Huerta Jaramillo
Samuel Cantu Cantu
Liga a las diapositivas:
Presentacion del proyecto III de algoritmos por rapidshare
Presentacion del proyecto III de algoritmos por megaupload
Definiré con mis propias palabras el termino recursion: bueno yo entendi que recursion es cuando un algoritmo se llama a si mismo dentro de ese algoritmo para completar un proceso, es decir, el algoritmo se divide en partes y se llama a la operacion para que haga los problemas de cada parte hasta que ya no queda nada que resolver y termina el algoritmo y sirve para resolver ciertos problemas como el maximo comun divisor (mcd) que es el tema que nos toco de este proyecto. La recursion segun lo que investigue en algoritmos que ocupan mucha memoria no es muy bueno porque como se divide el algoritmo en partes, el programa utiliza memoria para cada parte entonces el algoritmo ocuparia demasiada memoria.
Bueno como les dije anteriormente nos toco el proyecto del "Maximo Comun Divisor" (mcd).
Como trabajamos en grupo:
Bueno todos nos dividimos el trabajo en partes y cada quien hizo su trabajo, despues mis compañeros me enviaron lo que hicieron y yo lo puse en una presentación. Fue un proyecto facil porque todos trabajos en equipo y nos ayudabamos a resolver nuestras dudas.
Que fue mi contribucion al trabajo:
Mi contribucion fue hacer la presentacion en Powerpoint con todos los temas, ademas de hacer lo de los algoritmos iterativos y recursivos y hacer los ejemplos de ejecucion paso a paso y ayudar a mis compañeros en lo del analisis asintotico y algunas dudas mas.
Como compara lo que hice con lo que hicieron mis compañeros:
Bueno como dije anteriormente, todos nos dividimos el trabajo pero por falta de tiempo y planificacion a algunos les toco menos trabajo que hacer o mas trabajo.
Que podria mejorar en el futuro:
Como equipo podriamos mejor la planificacion del tiempo, empezar antes, para que no se nos juntara todo el trabajo en un solo dia.
Ligas a los blogs de mis compañeros:
Ernesto Mendez Govea
Alberto Huerta Jaramillo
Samuel Cantu Cantu
Liga a las diapositivas:
Presentacion del proyecto III de algoritmos por rapidshare
Presentacion del proyecto III de algoritmos por megaupload
5 de marzo de 2010
Proyecto II
Bueno yo escogi el algoritmo de PageRank. ¿Qué es PageRank? aqui tenemos una definicion de Wikipedia:
PageRank es una marca registrada y patentada por Google el 9 de enero de 1999 que ampara una familia de algoritmos utilizados para asignar de forma numérica la relevancia de los documentos (o páginas web) indexados por un motor de búsqueda.Es utilizado por el popular motor de búsqueda Google para ayudarle a determinar la importancia o relevancia de una página. Fue desarrollado por los fundadores de Google, Larry Page y Sergey Brin, en la Universidad de Stanford.
PageRank utiliza los enlaces o hiperviculos como un indicador de valor de una pagina. Google interpreta un enlace de una página A a una página B como un voto, de la página A, para la página B. Pero Google mira más allá del volumen de votos, o enlaces que una página recibe; también analiza la página que emite el voto. Los votos emitidos por las páginas consideradas "importantes", es decir con un PageRank elevado, valen más, y ayudan a hacer a otras páginas "importantes". Por lo tanto, el PageRank de una página refleja la importancia de la misma en Internet.
Vamos a definir el algoritmo anterior en forma matemática de la siguiente manera:
El peso o importancia de una página es el resultado de una "votación" entre todas las demás páginas de la World Wide Web acerca del nivel de importancia que tiene esa página. Un hiperenlace a una página cuenta como un voto de apoyo. El PageRank de una página se define recursivamente y depende del número y PageRank de todas las páginas que la enlazan. Una página que está enlazada por muchas páginas con un PageRank alto consigue también un PageRank alto. Si no hay enlaces a una página web, no hay apoyo a esa página específica. El PageRank de la barra de Google va de 0 a 10. Diez es el máximo PageRank posible y son muy pocos los sitios que gozan de esta calificación, 1 es la calificación mínima que recibe un sitio normal, y cero significa que el sitio ha sido penalizado o aún no ha recibido una calificación de PageRank. Parece ser una escala logarítmica. Los detalles exactos de esta escala son desconocidos.
Como vemos en la imagen las caras son las paginas de internet y las manos que apuntan son adonde se estan enlazando. También nos damos cuenta que la cara mas grande significa que es la pagina mas importante.
Continuamos con el problema y su solución optima:
De una red formada por ligas entre páginas, cuál página tiene el valor máximo dePageRank
Es muy dificil usar el algoritmo de Pagerank porque puede llegar a usar mas de 100 variables debido a que tiene mas de 100 factores a analizar pero pondre un ejemplo facil.
Tenemos un sitio con tres páginas, A, B y C, donde A enlaza B y C, B enlaza C, y C enlaza A. De acuerdo con el algoritmo, el factor aleatorio d es de 0.85, pero para simplificar los cálculos lo redondeamos a 0.5. Este factor d sabemos que afecta al PageRank, pero no afecta a los principios del PageRank. Así que hagamos unos cálculos:
PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) / 2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
Estas ecuaciones son sencillas. Nos queda el siguiente PageRank para cada página:
PR(A) = 14/13 = 1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 = 1.15384615
Como es obvio, el PageRank de la suma de las páginas es 3, igual que el número de páginas. Este resultado no es específico de nuestro sencillo ejemplo.
En nuestro caso es facil calcularlo directamente ya que solo tenemos 3 páginas. Pero actualmente los sitios están formados por miles de páginas, luego es necesario algún otro sistema de cálculo.
Como vemos la pagina C es la que tiene el PageRank mas alto como debe ser porque C enlaza con B y C, despues le sigue A que enlaza a B y C, y al último B que solo enlaza a C.
Despues formulamos el problema de decision:
¿Dado un conjunto de paginas web, sera posible encontrar una pagina web con mas indice de PageRank?
R=si, si la pagina que es mas enlazada de otras paginas y ademas que las paginas que la enzalan son importantes. Porque al comparar las paginas se analizan mas de 100 factores como lo habia dicho anteriormente y debe encontrar que la hace importante y asi darle un valor alto de PageRank.
Complejidad
En mi opinion este problema pertenece a P porque puede ser resuelto en una máquina determinista (computadora) en tiempo polinómico ya que Google en cuestion de segundos encuentra resultados, lo que corresponde intuitivamente a problemas que pueden ser resueltos aún en el peor de sus casos. Por eso tampoco es NP-dificil.
Datos:
Juan Manuel Casanova Villarreal
Matricula: 1453829
Grupo 4200 martes V4 a V6
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/PageRank
http://www.alegsa.com.ar/Dic/pagerank.php (imagen)
http://refugioantiaereo.com/2006/09/formula-pagerank-explicada
http://es.wikipedia.org/wiki/Complejidad_computacional
PageRank es una marca registrada y patentada por Google el 9 de enero de 1999 que ampara una familia de algoritmos utilizados para asignar de forma numérica la relevancia de los documentos (o páginas web) indexados por un motor de búsqueda.Es utilizado por el popular motor de búsqueda Google para ayudarle a determinar la importancia o relevancia de una página. Fue desarrollado por los fundadores de Google, Larry Page y Sergey Brin, en la Universidad de Stanford.
PageRank utiliza los enlaces o hiperviculos como un indicador de valor de una pagina. Google interpreta un enlace de una página A a una página B como un voto, de la página A, para la página B. Pero Google mira más allá del volumen de votos, o enlaces que una página recibe; también analiza la página que emite el voto. Los votos emitidos por las páginas consideradas "importantes", es decir con un PageRank elevado, valen más, y ayudan a hacer a otras páginas "importantes". Por lo tanto, el PageRank de una página refleja la importancia de la misma en Internet.
Vamos a definir el algoritmo anterior en forma matemática de la siguiente manera:
- PR(A) es el PageRank de la página A.
- d es un factor de amortiguación que tiene un valor entre 0 y 1.
- PR(i) son los valores de PageRank que tienen cada una de las las páginas i que enlazan a A.
- C(i) es el número total de enlaces salientes de la página i (sean o no hacia A).
El peso o importancia de una página es el resultado de una "votación" entre todas las demás páginas de la World Wide Web acerca del nivel de importancia que tiene esa página. Un hiperenlace a una página cuenta como un voto de apoyo. El PageRank de una página se define recursivamente y depende del número y PageRank de todas las páginas que la enlazan. Una página que está enlazada por muchas páginas con un PageRank alto consigue también un PageRank alto. Si no hay enlaces a una página web, no hay apoyo a esa página específica. El PageRank de la barra de Google va de 0 a 10. Diez es el máximo PageRank posible y son muy pocos los sitios que gozan de esta calificación, 1 es la calificación mínima que recibe un sitio normal, y cero significa que el sitio ha sido penalizado o aún no ha recibido una calificación de PageRank. Parece ser una escala logarítmica. Los detalles exactos de esta escala son desconocidos.
| Esquema gráfico del funcionamiento del PageRank de Google |
Continuamos con el problema y su solución optima:
De una red formada por ligas entre páginas, cuál página tiene el valor máximo dePageRank
Es muy dificil usar el algoritmo de Pagerank porque puede llegar a usar mas de 100 variables debido a que tiene mas de 100 factores a analizar pero pondre un ejemplo facil.
Tenemos un sitio con tres páginas, A, B y C, donde A enlaza B y C, B enlaza C, y C enlaza A. De acuerdo con el algoritmo, el factor aleatorio d es de 0.85, pero para simplificar los cálculos lo redondeamos a 0.5. Este factor d sabemos que afecta al PageRank, pero no afecta a los principios del PageRank. Así que hagamos unos cálculos:
PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) / 2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
Estas ecuaciones son sencillas. Nos queda el siguiente PageRank para cada página:
PR(A) = 14/13 = 1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 = 1.15384615
Como es obvio, el PageRank de la suma de las páginas es 3, igual que el número de páginas. Este resultado no es específico de nuestro sencillo ejemplo.
En nuestro caso es facil calcularlo directamente ya que solo tenemos 3 páginas. Pero actualmente los sitios están formados por miles de páginas, luego es necesario algún otro sistema de cálculo.
Como vemos la pagina C es la que tiene el PageRank mas alto como debe ser porque C enlaza con B y C, despues le sigue A que enlaza a B y C, y al último B que solo enlaza a C.
Despues formulamos el problema de decision:
¿Dado un conjunto de paginas web, sera posible encontrar una pagina web con mas indice de PageRank?
R=si, si la pagina que es mas enlazada de otras paginas y ademas que las paginas que la enzalan son importantes. Porque al comparar las paginas se analizan mas de 100 factores como lo habia dicho anteriormente y debe encontrar que la hace importante y asi darle un valor alto de PageRank.
Complejidad
En mi opinion este problema pertenece a P porque puede ser resuelto en una máquina determinista (computadora) en tiempo polinómico ya que Google en cuestion de segundos encuentra resultados, lo que corresponde intuitivamente a problemas que pueden ser resueltos aún en el peor de sus casos. Por eso tampoco es NP-dificil.
Datos:
Juan Manuel Casanova Villarreal
Matricula: 1453829
Grupo 4200 martes V4 a V6
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/PageRank
http://www.alegsa.com.ar/Dic/pagerank.php (imagen)
http://refugioantiaereo.com/2006/09/formula-pagerank-explicada
http://es.wikipedia.org/wiki/Complejidad_computacional
19 de febrero de 2010
Proyecto I continuación segundo algoritmo
Bueno como les comente aqui voy a seguir hablando del proyecto I con el problema 2.
Problema 2: Colocar un grupo de libros en un librero en orden alfabetico segun el titulo.
Diagrama de flujo
Bueno como vemos en la imagen anterior primero checamos si tienes libros en el librero, despues vemos lo que en programacion se llama switch en el que viene escrito cual es el orden que tienes, que escoges o escogiste y te pide seleccionar un caso de 3 posibles.
El primer caso es acomodar los libros por título, te pide tomar un libro, buscar la inicial del título, después buscar el lugar deonde va esa inicial en el librero, despues si existen muchos libros con esa inicial busca cada letra del titulo para encontrarle un lugar, despues colócalo alli.
El segundo caso es por autor, toma un libro y busca el nombre del autor, despues en el librero busca el lugar donde va ese autor, si existen muchos libros, busca algun número o el nombre del libro, despues busca el lugar correcto en orden alfabetico y finalmente colocalo alli.
El tercer y ultimo caso es acomodar los libros por editorial, toma un libro y busca la inicial del nombre de la editorial, busca el lugar donde va esa editorial, si hay uno o mas libros en el librero acomodalo segun el titulo y eso va a hacer que te regreses al punto 2 que es acomodar por titulo.
Si tienes mas libros por acomodar vas a tener que regresar al punto 1, y si no, haz terminado.
El programa y el codigo en C:
#include
#include
int opcion;
int main()
{
printf("Acerca los libros que quieres acomodar en el librero\n");
do{
printf("\nTienes libros en el librero?\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
}while(opcion!=1
opcion!=2);
do{
do{
printf("\nQue orden tienes, escoges o escogiste?\n1.-Titulo\n2.-Autor\n3.-Editorial\n");
scanf("%d",&opcion);
}while(opcion<1
opcion>3);
clrscr();
do
switch(opcion)
{
case 1: {
printf("\nPOR TITULO\n");
getch();
printf("Toma un libro\n");
getch();
printf("BUsca la inicial del titulo\n");
getch();
printf("En el librero busca el lugar donde va esa inicial\n");
getch();
printf("Si existen muchos libros alli, busca cada letra\ndel titulo del libro para encontrarle un lugar\n");
getch();
opcion=0;
break;
}
case 2: {
printf("\nPOR AUTOR\n");
printf("Toma un libro busca el nombre del autor\n");
printf("En el librero busca el lugar donde va ese autor");
printf("\n\nSi existen muchos libros alli, busca algun numero o el nombre del titulo\n");
printf("Busca el lugar correcto de acuerdo al numero o a la inicial del titulo, en orden alfabetico\n");
opcion=0;
break;
}
case 3: {
printf("\nPOR EDITORIAL\n");
printf("\ntoma un libro, busca la inical del nombre de la editorial\n");
printf("\nEn el librero busca el lugar donde va esa editorial\n");
printf("\nHay uno o mas libros\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
if(opcion==2)
break;
else{
opcion=2;
break;
}
}
}
}while(opcion==2);
printf("\nColocala alli\n");
clrscr();
printf("\nTienes mas libros para acomodar\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
}while(opcion==1);
printf("\nHaz Terminado\n");
}
2 ejemplos de ejecucion paso a paso:
Ejemplo 1:
Voy a inventar nombres
Tenemos el libro "Serpiente" de Jesus Ruiz de la editorial Corona
Lo acomodaremos por título, buscas la inicial del titulo que es la "S", buscas en el librero donde va esa inicial, despues si existen muchos libros con esa inicial busca cada letra del titulo para encontrarle un lugar, despues colocalo allí.
Ejemplo 2:
Tenemos el libro "Tigre" de Gonzalo Solis de la editorial Corona
Lo acomodaremos por autor, busca el nombre del autor, despues en el librero busca el lugar donde va ese autor, si existen muchos libros con ese autor, puedes acomodarlo por titulo o editorial tambien, despues buscael lugar correcto en orden alfabetico y finalmente colocalo allí.
Bueno estas dos entradas son el Proyecto I
Problema 2: Colocar un grupo de libros en un librero en orden alfabetico segun el titulo.
Diagrama de flujo
Bueno como vemos en la imagen anterior primero checamos si tienes libros en el librero, despues vemos lo que en programacion se llama switch en el que viene escrito cual es el orden que tienes, que escoges o escogiste y te pide seleccionar un caso de 3 posibles.
El primer caso es acomodar los libros por título, te pide tomar un libro, buscar la inicial del título, después buscar el lugar deonde va esa inicial en el librero, despues si existen muchos libros con esa inicial busca cada letra del titulo para encontrarle un lugar, despues colócalo alli.
El segundo caso es por autor, toma un libro y busca el nombre del autor, despues en el librero busca el lugar donde va ese autor, si existen muchos libros, busca algun número o el nombre del libro, despues busca el lugar correcto en orden alfabetico y finalmente colocalo alli.
El tercer y ultimo caso es acomodar los libros por editorial, toma un libro y busca la inicial del nombre de la editorial, busca el lugar donde va esa editorial, si hay uno o mas libros en el librero acomodalo segun el titulo y eso va a hacer que te regreses al punto 2 que es acomodar por titulo.
Si tienes mas libros por acomodar vas a tener que regresar al punto 1, y si no, haz terminado.
El programa y el codigo en C:
#include
#include
int opcion;
int main()
{
printf("Acerca los libros que quieres acomodar en el librero\n");
do{
printf("\nTienes libros en el librero?\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
}while(opcion!=1
opcion!=2);
do{
do{
printf("\nQue orden tienes, escoges o escogiste?\n1.-Titulo\n2.-Autor\n3.-Editorial\n");
scanf("%d",&opcion);
}while(opcion<1
opcion>3);
clrscr();
do
switch(opcion)
{
case 1: {
printf("\nPOR TITULO\n");
getch();
printf("Toma un libro\n");
getch();
printf("BUsca la inicial del titulo\n");
getch();
printf("En el librero busca el lugar donde va esa inicial\n");
getch();
printf("Si existen muchos libros alli, busca cada letra\ndel titulo del libro para encontrarle un lugar\n");
getch();
opcion=0;
break;
}
case 2: {
printf("\nPOR AUTOR\n");
printf("Toma un libro busca el nombre del autor\n");
printf("En el librero busca el lugar donde va ese autor");
printf("\n\nSi existen muchos libros alli, busca algun numero o el nombre del titulo\n");
printf("Busca el lugar correcto de acuerdo al numero o a la inicial del titulo, en orden alfabetico\n");
opcion=0;
break;
}
case 3: {
printf("\nPOR EDITORIAL\n");
printf("\ntoma un libro, busca la inical del nombre de la editorial\n");
printf("\nEn el librero busca el lugar donde va esa editorial\n");
printf("\nHay uno o mas libros\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
if(opcion==2)
break;
else{
opcion=2;
break;
}
}
}
}while(opcion==2);
printf("\nColocala alli\n");
clrscr();
printf("\nTienes mas libros para acomodar\n1.-Si\n2.-No\n");
scanf("%d",&opcion);
}while(opcion==1);
printf("\nHaz Terminado\n");
}
2 ejemplos de ejecucion paso a paso:
Ejemplo 1:
Voy a inventar nombres
Tenemos el libro "Serpiente" de Jesus Ruiz de la editorial Corona
Lo acomodaremos por título, buscas la inicial del titulo que es la "S", buscas en el librero donde va esa inicial, despues si existen muchos libros con esa inicial busca cada letra del titulo para encontrarle un lugar, despues colocalo allí.
Ejemplo 2:
Tenemos el libro "Tigre" de Gonzalo Solis de la editorial Corona
Lo acomodaremos por autor, busca el nombre del autor, despues en el librero busca el lugar donde va ese autor, si existen muchos libros con ese autor, puedes acomodarlo por titulo o editorial tambien, despues buscael lugar correcto en orden alfabetico y finalmente colocalo allí.
Bueno estas dos entradas son el Proyecto I
Suscribirse a:
Comentarios (Atom)