El algoritmo de Euclides es un método antiguo y eficaz para calcular el máximo común divisor (MCD). Fue originalmente descrito por Euclides en su obra Elementos. El algoritmo de Euclides extendido es una ligera modificación que permite además expresar al máximo común divisor como una combinación lineal. Este algoritmo tiene aplicaciones en diversas áreas como álgebra, teoría de números y ciencias de la computación entre otras. Con unas ligeras modificaciones suele ser utilizado en computadoras electrónicas debido a su gran eficiencia.
Al dividir a entre b (números enteros), se obtiene un cociente q y un residuo r. Es posible demostrar que el máximo común divisor de a y b es el mismo que el de b y r. Éste es el fundamento principal del algoritmo. También es importante tener en cuenta que el máximo común divisor de cualquier número a y 0 es precisamente a. Para fines prácticos, la notación mcd(a,b) significa máximo común divisor de a y b.
Según lo antes mencionado, para calcular el máximo común divisor de 2366 y 273 se puede proseguir de la siguiente manera:
Paso Operación Significado
1 2366 dividido entre 273 es 8 y sobran 182 mcd(2366,273) = mcd(273,182)
2 273 dividido entre 182 es 1 y sobran 91 mcd(273,182) = mcd(182,91)
3 182 dividido entre 91 es 2 y sobra 0 mcd(182,91) = mcd(91,0)
La secuencia de igualdades mcd(2366,273) = mcd(273,182) = mcd(182,91) = mcd(91,0) implican que mcd(2366,273) = mcd(91,0). Dado que mcd(91,0) = 91, entonces se concluye que mcd(2366,273) = 91. Este mismo procedimiento se puede aplicar a cualesquiera dos números naturales. En general, si se desea encontrar el máximo común divisor de dos números naturales a y b, se siguen las siguientes reglas:
1.Si b = 0 entonces mcd(a,b) = a y el algoritmo termina
2.En otro caso, mcd(a,b) = mcd(b,r) donde r es el resto de dividir a entre b. Para calcular mcd(b,r) se utilizan estas mismas reglas.
Aqui tenemos el pseudocodigo:
Función mcd(a,b):
Mientras
haga lo siguiente:
El resultado es a
Otro ejemplo sencillo:
MCD 12345 y 6789
12345mod789= 510
789mod510=279
510mod279=231
279mod231=48
231mod48=39
48mod39=9
39mod9=3
9mod3=0
MCD (3,0) entonces como tenemos b=0, el MCD es a=3.
Como vemos este es un algoritmo sencillo para obtener el MCD de dos numeros.
Complejidad: El teorema de Lamé afirma que el caso peor para este algoritmo es cuando se le pide calcular el máximo común divisor de dos números consecutivos de la sucesión de Fibonacci. En general, el número de divisiones efectuadas por el algoritmo nunca supera 5 veces el número de dígitos que tienen estos números. En términos de complejidad computacional, esto significa que se requieren
divisiones para calcular el máximo común divisor de n y m donde n> m.
El número promedio de divisiones efectuadas por el algoritmo se estuvo investigando desde 1968, pero sólo hasta apenas el año 2002, Brigitte Vallée demostró que si los dos números se pueden representar con n bits, entonces el número promedio de divisiones necesarias es:
Sin embargo, no basta con saber el número de divisiones. Hay que recordar que el algoritmo de Euclides funciona tanto para polinomios como para números enteros, y en general, cualquier dominio Euclídeo. En cada caso, la complejidad del algoritmo depende del número de divisiones efectuadas y del costo de cada división. En el caso de los polinomios, el número de divisiones es 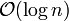 donde n es el grado de los polinomios.
donde n es el grado de los polinomios.
Bibliografia:
http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829
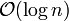 donde n es el grado de los polinomios.
donde n es el grado de los polinomios.Bibliografia:
http://es.wikipedia.org/wiki/Algoritmo_de_Euclides
Nombre: Juan Manuel Casanova Villarreal
Matricula: 1453829




No hay comentarios:
Publicar un comentario