Proyecto V

Bueno el tema que escogi para este proyecto V fue "Arboles de expansion: algoritmo de Kruskal.
Bueno para entender mejor sobre los arboles de expansion y algoritmo de kruskal tenemos estas definiciones:
¿Que es un arbol de expansion? Un árbol de expansión T de un grafo conexo, no dirigido G es un árbol compuesto por todos los vértices y algunas (quizá todas) de las aristas de G. Informalmente, un árbol de expansión de G es una selección de aristas de G que forman un árbol que cubre todos los vértices. Esto es, cada vértice está en el árbol, pero no hay ciclos.

Aqui hay una imagen de un arbol de expansion

¿Que es el algoritmo de Kruskal? Esta es la definicion: El algoritmo de Kruskal es un algoritmo de la teoría de grafos para encontrar un árbol de expansión mínimo en un grafo conexo y ponderado. Es decir, busca un subconjunto de aristas que, formando un árbol, incluyen todos los vértices y no hay ciclos y donde el valor total de todas las aristas del árbol es el mínimo, a esto se le llama arbol de expansion minimo. El algoritmo de Kruskal es un ejemplo de algoritmo voraz. Esta definicion en términos simples es como encontrar el arbol de expansion pero que el peso total de las aristas sea el menor posible.
Bueno ahora ¿que es un algoritmo voraz? Un algoritmo voraz es un algoritmo que trabaja por etapas, en cada una de estas etapas toma la decisión que le parece mejor para encontrar una solución optima en cada etapa sin pensar en las consecuencias futuras, esto hace que si en cada etapa hay una solución optima, supone que habrá una solución optima global del problema.

Pero no siempre es así, no todos los problemas pueden ser resueltos por este tipo de algoritmos. La estrategia de este tipo de algoritmos consiste en tratar de ganar todas las batallas sin pensar que para ganar la guerra muchas veces es necesario perder alguna batalla. Pero para este tipo de problemas siempre hay una solución optima.

Ya vimos todas las definiciones pero para que nos sirve el algoritmo de kruskal, sabemos que con el podemos encontrar el arbol de expansion minimo pero para que nos sirve esto en la vida cotidiana. La aplicación típica de este problema es el diseño de redes telefónicas. Un ejemplo seria: Una empresa con diferentes oficinas, trata de trazar líneas de teléfono para conectarlas unas con otras.La compañía telefónica le ofrece esta interconexión, pero ofrece tarifas diferentes o costes por conectar cada par de oficinas. Cómo conectar entonces las oficinas al mínimo coste total.
La formulación del árbol de expansion minimo también ha sido aplicada para hallar soluciones en diversas áreas (diseño de redes de transporte, diseño de redes de telecomunicaciones - TV por cable, sistemas distribuidos, interpretación de datos climatológicos, visión artificial - análisis de imágenes - extracción de rasgos de parentesco, análisis de clusters y búsqueda de superestructuras de quasar, plegamiento de proteínas, reconocimiento de células cancerosas, y otros).

A continuacion tenemos el ejemplo a paso a paso de como funciona este algoritmo:

 

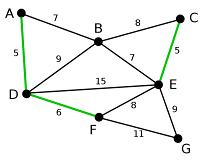
Este es el grafo original. Los números de las aristas indican su peso. Ninguna de las aristas está resaltada.

AD y CE son las aristas más cortas, con peso 5, y AD se ha elegido arbitrariamente, por tanto se resalta.

 

Sin embargo, ahora es CE la arista más pequeña que no forma ciclos, con peso 5, por lo que se resalta como segunda arista. 

La siguiente arista, DF con peso 6, ha sido resaltada utilizando el mismo método.

La siguientes aristas más pequeñas son AB y BE, ambas con peso 7. AB se elige arbitrariamente, y se resalta. La arista BD se resalta en rojo, porque formaría un ciclo ABD si se hubiera elegido.

El proceso continúa marcando las aristas, BE con peso 7. Muchas otras aristas se marcan en rojo en este paso: BC (formaría el ciclo BCE), DE (formaría el ciclo DEBA), y FE (formaría el ciclo FEBAD).

Finalmente, el proceso termina con la arista EG de peso 9, y se ha encontrado el árbol de expansion mínimo.





Aqui tenemos un video de youtube que nos pueden ayudar a comprender mejor el tema

---Ahora sigue su definicion formal en problema de decision:

¿Puede el algoritmo de Kruskal encontrar siempre el arbol de expansion minima? R= si

Segun lo que definimos anteriormente el algoritmo de Kruskal siempre tiene una solucion optima a este tipo de problemas donde se busca el arbol de expansion minimo eso quiere decir que este algoritmo pertenece a P porque se puede resolver de forma eficiente por una maquina determinista en tiempo polinomial.

---Analisis asintotico:

m el número de aristas del grafo y n el número de vértices, el algoritmo de Kruskal muestra una complejidad O(m log m) o, equivalentemente, O(m log n), cuando se ejecuta sobre estructuras de datos simples. Los tiempos de ejecución son equivalentes porque:

m es a lo sumo n2 y log n2 = 2logn es O(log n).
Ignorando los vértices aislados, los cuales forman su propia componente del árbol de expansión mínimo, n ≤ 2m, así que log n es O(log m).Se puede conseguir esta complejidad de la siguiente manera: primero se ordenan las aristas por su peso usando una ordenación por comparación (comparison sort) con una complejidad del orden de O(m log m); esto permite que el paso "eliminar una arista de peso mínimo de C" se ejecute en tiempo constante. Lo siguiente es usar una estructura de datos sobre conjuntos disjuntos  para controlar qué vértices están en qué componentes. Es necesario hacer orden de O(m) operaciones ya que por cada arista hay dos operaciones de búsqueda y posiblemente una unión de conjuntos. Incluso una estructura de datos sobre conjuntos disjuntos simple con uniones por rangos puede ejecutar las operaciones mencionadas en O(m log n). Por tanto, la complejidad total es del orden de O(m log m) = O(m log n).

---Ahora tenemos el pseudocodigo:
Se crea un bosque B (un conjunto de árboles), donde cada vértice del grafo es un árbol separado.
Se crea un conjunto C que contenga a todas las aristas del grafo.
Mientras C es no vacío .
Eliminar una arista de peso mínimo de C.
Si esa arista conecta dos árboles diferentes se añade al bosque, combinando los dos árboles en un solo árbol.
En caso contrario, se desecha la arista.
Al acabar el algoritmo, el bosque tiene un solo componente, el cual forma un árbol de expansión mínimo del grafo.

---Estructuras que utiliza
Pues este algoritmo usa arreglos, árboles por supuesto

Bibliografia:

http://personales.upv.es/arodrigu/Grafos/Kruskal.htm

http://es.wikipedia.org/wiki/Algoritmo_de_Kruskal

http://es.wikipedia.org/wiki/%C3%81rbol_de_expansi%C3%B3n

Enlace a la presentacion interactiva:

http://rapidshare.com/files/387870056/arboles_de_expansi__n--_algoritmo_de_Kruskal.ppt.html

Juan Manuel Casanova Villarreal
Matricula: 1453829