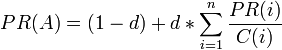Este es el proyecto III que habla del tema de recursion.
Definiré con mis propias palabras el termino recursion: bueno yo entendi que recursion es cuando un algoritmo se llama a si mismo dentro de ese algoritmo para completar un proceso, es decir, el algoritmo se divide en partes y se llama a la operacion para que haga los problemas de cada parte hasta que ya no queda nada que resolver y termina el algoritmo y sirve para resolver ciertos problemas como el maximo comun divisor (mcd) que es el tema que nos toco de este proyecto. La recursion segun lo que investigue en algoritmos que ocupan mucha memoria no es muy bueno porque como se divide el algoritmo en partes, el programa utiliza memoria para cada parte entonces el algoritmo ocuparia demasiada memoria.
Bueno como les dije anteriormente nos toco el proyecto del "Maximo Comun Divisor" (mcd).
Como trabajamos en grupo:
Bueno todos nos dividimos el trabajo en partes y cada quien hizo su trabajo, despues mis compañeros me enviaron lo que hicieron y yo lo puse en una presentación. Fue un proyecto facil porque todos trabajos en equipo y nos ayudabamos a resolver nuestras dudas.
Que fue mi contribucion al trabajo:
Mi contribucion fue hacer la presentacion en Powerpoint con todos los temas, ademas de hacer lo de los algoritmos iterativos y recursivos y hacer los ejemplos de ejecucion paso a paso y ayudar a mis compañeros en lo del analisis asintotico y algunas dudas mas.
Como compara lo que hice con lo que hicieron mis compañeros:
Bueno como dije anteriormente, todos nos dividimos el trabajo pero por falta de tiempo y planificacion a algunos les toco menos trabajo que hacer o mas trabajo.
Que podria mejorar en el futuro:
Como equipo podriamos mejor la planificacion del tiempo, empezar antes, para que no se nos juntara todo el trabajo en un solo dia.
Ligas a los blogs de mis compañeros:
Ernesto Mendez Govea
Alberto Huerta Jaramillo
Samuel Cantu Cantu
Liga a las diapositivas:
Presentacion del proyecto III de algoritmos por rapidshare
Presentacion del proyecto III de algoritmos por megaupload
21 de marzo de 2010
5 de marzo de 2010
Proyecto II
Bueno yo escogi el algoritmo de PageRank. ¿Qué es PageRank? aqui tenemos una definicion de Wikipedia:
PageRank es una marca registrada y patentada por Google el 9 de enero de 1999 que ampara una familia de algoritmos utilizados para asignar de forma numérica la relevancia de los documentos (o páginas web) indexados por un motor de búsqueda.Es utilizado por el popular motor de búsqueda Google para ayudarle a determinar la importancia o relevancia de una página. Fue desarrollado por los fundadores de Google, Larry Page y Sergey Brin, en la Universidad de Stanford.
PageRank utiliza los enlaces o hiperviculos como un indicador de valor de una pagina. Google interpreta un enlace de una página A a una página B como un voto, de la página A, para la página B. Pero Google mira más allá del volumen de votos, o enlaces que una página recibe; también analiza la página que emite el voto. Los votos emitidos por las páginas consideradas "importantes", es decir con un PageRank elevado, valen más, y ayudan a hacer a otras páginas "importantes". Por lo tanto, el PageRank de una página refleja la importancia de la misma en Internet.
Vamos a definir el algoritmo anterior en forma matemática de la siguiente manera:
El peso o importancia de una página es el resultado de una "votación" entre todas las demás páginas de la World Wide Web acerca del nivel de importancia que tiene esa página. Un hiperenlace a una página cuenta como un voto de apoyo. El PageRank de una página se define recursivamente y depende del número y PageRank de todas las páginas que la enlazan. Una página que está enlazada por muchas páginas con un PageRank alto consigue también un PageRank alto. Si no hay enlaces a una página web, no hay apoyo a esa página específica. El PageRank de la barra de Google va de 0 a 10. Diez es el máximo PageRank posible y son muy pocos los sitios que gozan de esta calificación, 1 es la calificación mínima que recibe un sitio normal, y cero significa que el sitio ha sido penalizado o aún no ha recibido una calificación de PageRank. Parece ser una escala logarítmica. Los detalles exactos de esta escala son desconocidos.
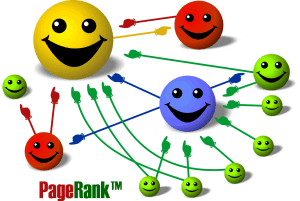
Como vemos en la imagen las caras son las paginas de internet y las manos que apuntan son adonde se estan enlazando. También nos damos cuenta que la cara mas grande significa que es la pagina mas importante.
Continuamos con el problema y su solución optima:
De una red formada por ligas entre páginas, cuál página tiene el valor máximo dePageRank
Es muy dificil usar el algoritmo de Pagerank porque puede llegar a usar mas de 100 variables debido a que tiene mas de 100 factores a analizar pero pondre un ejemplo facil.
Tenemos un sitio con tres páginas, A, B y C, donde A enlaza B y C, B enlaza C, y C enlaza A. De acuerdo con el algoritmo, el factor aleatorio d es de 0.85, pero para simplificar los cálculos lo redondeamos a 0.5. Este factor d sabemos que afecta al PageRank, pero no afecta a los principios del PageRank. Así que hagamos unos cálculos:
PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) / 2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
Estas ecuaciones son sencillas. Nos queda el siguiente PageRank para cada página:
PR(A) = 14/13 = 1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 = 1.15384615
Como es obvio, el PageRank de la suma de las páginas es 3, igual que el número de páginas. Este resultado no es específico de nuestro sencillo ejemplo.
En nuestro caso es facil calcularlo directamente ya que solo tenemos 3 páginas. Pero actualmente los sitios están formados por miles de páginas, luego es necesario algún otro sistema de cálculo.
Como vemos la pagina C es la que tiene el PageRank mas alto como debe ser porque C enlaza con B y C, despues le sigue A que enlaza a B y C, y al último B que solo enlaza a C.
Despues formulamos el problema de decision:
¿Dado un conjunto de paginas web, sera posible encontrar una pagina web con mas indice de PageRank?
R=si, si la pagina que es mas enlazada de otras paginas y ademas que las paginas que la enzalan son importantes. Porque al comparar las paginas se analizan mas de 100 factores como lo habia dicho anteriormente y debe encontrar que la hace importante y asi darle un valor alto de PageRank.
Complejidad
En mi opinion este problema pertenece a P porque puede ser resuelto en una máquina determinista (computadora) en tiempo polinómico ya que Google en cuestion de segundos encuentra resultados, lo que corresponde intuitivamente a problemas que pueden ser resueltos aún en el peor de sus casos. Por eso tampoco es NP-dificil.
Datos:
Juan Manuel Casanova Villarreal
Matricula: 1453829
Grupo 4200 martes V4 a V6
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/PageRank
http://www.alegsa.com.ar/Dic/pagerank.php (imagen)
http://refugioantiaereo.com/2006/09/formula-pagerank-explicada
http://es.wikipedia.org/wiki/Complejidad_computacional
PageRank es una marca registrada y patentada por Google el 9 de enero de 1999 que ampara una familia de algoritmos utilizados para asignar de forma numérica la relevancia de los documentos (o páginas web) indexados por un motor de búsqueda.Es utilizado por el popular motor de búsqueda Google para ayudarle a determinar la importancia o relevancia de una página. Fue desarrollado por los fundadores de Google, Larry Page y Sergey Brin, en la Universidad de Stanford.
PageRank utiliza los enlaces o hiperviculos como un indicador de valor de una pagina. Google interpreta un enlace de una página A a una página B como un voto, de la página A, para la página B. Pero Google mira más allá del volumen de votos, o enlaces que una página recibe; también analiza la página que emite el voto. Los votos emitidos por las páginas consideradas "importantes", es decir con un PageRank elevado, valen más, y ayudan a hacer a otras páginas "importantes". Por lo tanto, el PageRank de una página refleja la importancia de la misma en Internet.
Vamos a definir el algoritmo anterior en forma matemática de la siguiente manera:
- PR(A) es el PageRank de la página A.
- d es un factor de amortiguación que tiene un valor entre 0 y 1.
- PR(i) son los valores de PageRank que tienen cada una de las las páginas i que enlazan a A.
- C(i) es el número total de enlaces salientes de la página i (sean o no hacia A).
El peso o importancia de una página es el resultado de una "votación" entre todas las demás páginas de la World Wide Web acerca del nivel de importancia que tiene esa página. Un hiperenlace a una página cuenta como un voto de apoyo. El PageRank de una página se define recursivamente y depende del número y PageRank de todas las páginas que la enlazan. Una página que está enlazada por muchas páginas con un PageRank alto consigue también un PageRank alto. Si no hay enlaces a una página web, no hay apoyo a esa página específica. El PageRank de la barra de Google va de 0 a 10. Diez es el máximo PageRank posible y son muy pocos los sitios que gozan de esta calificación, 1 es la calificación mínima que recibe un sitio normal, y cero significa que el sitio ha sido penalizado o aún no ha recibido una calificación de PageRank. Parece ser una escala logarítmica. Los detalles exactos de esta escala son desconocidos.
| Esquema gráfico del funcionamiento del PageRank de Google |
Continuamos con el problema y su solución optima:
De una red formada por ligas entre páginas, cuál página tiene el valor máximo dePageRank
Es muy dificil usar el algoritmo de Pagerank porque puede llegar a usar mas de 100 variables debido a que tiene mas de 100 factores a analizar pero pondre un ejemplo facil.
Tenemos un sitio con tres páginas, A, B y C, donde A enlaza B y C, B enlaza C, y C enlaza A. De acuerdo con el algoritmo, el factor aleatorio d es de 0.85, pero para simplificar los cálculos lo redondeamos a 0.5. Este factor d sabemos que afecta al PageRank, pero no afecta a los principios del PageRank. Así que hagamos unos cálculos:
PR(A) = 0.5 + 0.5 PR(C)
PR(B) = 0.5 + 0.5 (PR(A) / 2)
PR(C) = 0.5 + 0.5 (PR(A) / 2 + PR(B))
Estas ecuaciones son sencillas. Nos queda el siguiente PageRank para cada página:
PR(A) = 14/13 = 1.07692308
PR(B) = 10/13 = 0.76923077
PR(C) = 15/13 = 1.15384615
Como es obvio, el PageRank de la suma de las páginas es 3, igual que el número de páginas. Este resultado no es específico de nuestro sencillo ejemplo.
En nuestro caso es facil calcularlo directamente ya que solo tenemos 3 páginas. Pero actualmente los sitios están formados por miles de páginas, luego es necesario algún otro sistema de cálculo.
Como vemos la pagina C es la que tiene el PageRank mas alto como debe ser porque C enlaza con B y C, despues le sigue A que enlaza a B y C, y al último B que solo enlaza a C.
Despues formulamos el problema de decision:
¿Dado un conjunto de paginas web, sera posible encontrar una pagina web con mas indice de PageRank?
R=si, si la pagina que es mas enlazada de otras paginas y ademas que las paginas que la enzalan son importantes. Porque al comparar las paginas se analizan mas de 100 factores como lo habia dicho anteriormente y debe encontrar que la hace importante y asi darle un valor alto de PageRank.
Complejidad
En mi opinion este problema pertenece a P porque puede ser resuelto en una máquina determinista (computadora) en tiempo polinómico ya que Google en cuestion de segundos encuentra resultados, lo que corresponde intuitivamente a problemas que pueden ser resueltos aún en el peor de sus casos. Por eso tampoco es NP-dificil.
Datos:
Juan Manuel Casanova Villarreal
Matricula: 1453829
Grupo 4200 martes V4 a V6
Referencias Bibliográficas:
http://es.wikipedia.org/wiki/PageRank
http://www.alegsa.com.ar/Dic/pagerank.php (imagen)
http://refugioantiaereo.com/2006/09/formula-pagerank-explicada
http://es.wikipedia.org/wiki/Complejidad_computacional
Suscribirse a:
Comentarios (Atom)